Design of Sawn Timber Beams or Joists
Courses > Timber Design > Design of Timber Members > Design of Sawn Timber Beams or Joists
Introduction
A timber beam may consist of a single member or may be built up from two or more members, called built up beams. • Timber beams are designed to resist- 1. Maximum bending moment 2. Maximum horizontal shear stress 3. Maximum stress at bearing.
Concepts and Formulas
Design requirement
-
Maximum bending stress, fb must not exceed allowable stress parallel to grain,
F'b = Fb*CD*CM*Ct*CF*CV*Cfu*Cr*Cc*Cf
Where
Fb is allowable bending stress in NDS supplement.
CD is load duration factor, (see NDS Table 2.3.2 reproduced below)
CM is wet service factor, (use when moisture of timber is higher than 19%)
Ct is temperature factor, (when timber is used in temperature higher than 150°F)
CL is beam stability factor, (See below)
CF is size factor, (apply only to visually graded sawn lumber members, and to round timber bending members, not apply simultaneously with Cv for glued laminated timber)
CV is volume factor, (apply only to glued laminated timber bending member)
Cfu is flat use factor, (when 2”-4” timber is loaded at wide face)
Cr is repetitive member factor, (apply to dimension bending member 2”-4” thick)
Cc is curvature factor (apply to curved glued laminated bending member)
Cf is form factor. (for round or diamond section)
-
Deflection should not exceed allowable limit. The elastic modulus shall be calculated as E'=E*CM*Ct, Where E is modulus of elasticity in NDS supplement
-
Maximum shear stress, fv shall not exceed allowable shear stress,
F'v = Fv*CD*CM*Ct*CH
Where Fv is allowable shear stress in NDS supplement and,
CH is shear stress factor depends on length of split and shake. Value of CH varies from 2 for no split to 1 with 1-1/2 split.
Adjustment factors
Load duration factor, CD
|
Load duration |
CD |
Design load |
|---|---|---|
|
Permanent |
0.9 |
Dead load |
|
Ten years |
1.0 |
Occupancy live load |
|
Two months |
1.15 |
Snow load |
|
Seven days |
1.25 |
Construction load |
|
Ten minutes |
1.6 |
Wind/Earthquake load |
|
Impact |
2.0 |
Impact load |
Beam stability factor, CL.
CL = 1 for the following condition for member, with nominal depth, B and width, D.
-
D/B £ 2
-
2 < D/B £ 4 – solid blocking is provided at both ends of member.
-
D/B = 5, one edge (tension or compression) is fully supported.
-
D/B = 6, bridge, full depth blocking, cross bracing at 8 ft maximum, and both edges are fully supported or compressive edge is fully supported to prevent lateral displacement, and the ends at the point of bearing are laterally supported to prevent rotation;
-
D/B = 7, both edge fully supported.
When the conditions were not met, CL is calculated based on a complicated equation in NDS section 3.3.3.7. Normally, it is easier to meet the requirement then to go through the complicated equation.
Size factor, CF
The size, CF, for timber species other than southern pine are listed in Table 4-A. For southern pine 2” to 4” thick, size factor needs not be applied. For southern pine 4” thick, 8” and wider, CF = 1.1. For dimension lumber, wider than 12”, CF = 0.9 except Dense structural 86. 72, and 65. in which, CF =0.9. When the depth of Dense structural 86, 72, and 65, dimension lumber exceeds 12”, CF =(12/d)1/9.
Repetitive member factor, Cr
Cr applies to dimension lumber 2” to 4” thick that subjected to bending. Cr =1.15 when members are used as joist, truss chords, rafters, etc and spacing is not exceed 24” and not less than 3”.
Wet service factor, CM
When the moisture of dimension lumber exceeds 19%, the design value Fb shall be multiplied by CM = 0.85 except that when Fb * CM £ 1500 psi, CM =1.
Design procedure for Timber Beam and Joist
-
Calculate design load and moment
-
Select timber species and cross section. Determine maximum bending stress, f”b=M/S, where M is design moment with load duration factor, S is section modulus.
-
Determine allowable bending stress, with the rest of multiplication factors
F"b = Fb*CD*CM*Ct*CF*CV*Cfu*Cr*Cc*Cf
-
Calculate elastic modulus
E'=E*CM*Ct
-
Calculate deflection of beam with load without load duration factor.
-
Calculate shear stress, f”v = VQ/Ib or for rectangular member, f”v = 3V/2b
Where, V is shear force with load duration factor, Q is first moment of inertia, I is second moment of inertia, b is width of the member, d is depth of the member.
-
Calculate allowable shear stress with the rest of multiplication factors
F"v = Fv*CD*CM*Ct*CH
Watch Videos
No videos available for this topic. 
Solved sample problems
-
Solved Example: Design of 2x12 Timber Floor Joist with Douglas Fir-Larch
-
Solved Example: Design of 2x10 Timber Floor Joist with Southern Pine
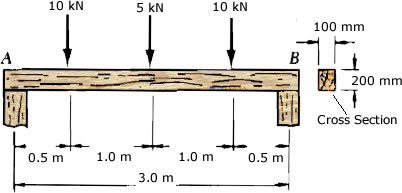
- Solved Example: Design of 3-3x12 Timber Beam with Southern Pine
Download Files
Read also
- Solved Example: Design of 3-3x12 Timber Beam with Southern Pine
- Solved Example: Design of 2x10 Timber Floor Joist with Southern Pine
- Solved Example: Design of 2x12 Timber Floor Joist with Douglas Fir-Larch
- Design of Sawn Timber Columns and Compressive Members
- Solved Example: Design of Sawn Timber Column
Share
Follow our official Facebook page (@civilengineeringbible) and Twitter page (@CivilEngBible) and do not miss the best civil engineering tools and articles!