Solved Example: Design of 3-3x12 Timber Beam with Southern Pine

Articles > Solved Example: Design of 3-3x12 Timber Beam with Southern Pine

Question:

Design data:

Length of beam: L = 16 ft

Tributary width: s = 8 ft

Top of beam supported by floor joists at 16 in O.C.

Design load:

Floor live load: W_L = 40 psf

Floor dead load: W_D = 10 psf

Superimposed dead load including mechanical and electric load, W_SD = 8 psf

Timber: Southern pine, moisture less than 19%, used in normal room temperature.

Solution:

Refer to Design of Sawn Timber Beams or Joists article for the concepts.

Calculate Design load: W = [(W_D + W_SD+ W_L]*s = 464 lb/ft

Design moment: M = W*L²/8 = 14850 lb-ft

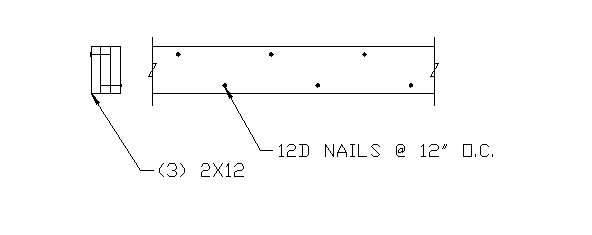
Use 3-3x12 nailed together with 12d nails at 12 in O.C. from both sides staggered.

Nominal dimension, B = 9 in, D = 12 in

Actual dimension, b = 7.5 in, d = 11.25 in

Section modulus: S = 158.2 in³, Modulus of inertia, I = 890 in⁴.

Bending stress: f_b =M/S = 1126 psi

Try Southern pine No. 2, F_b = 1500 psi

The depth to width ratio based on nominal dimension, D/B = 1.33

Since compressive edge is supported by floor joist at 16 in O.C., C_L = 1

Wet service factor: C_M = 1

Temperature factor: C_t = 1

Load duration factor for dead load: C_D = 0.9

Load duration factors for live load: C_D = 1.0

Other factors not applicable

Allowable stress, F’_b = F_b* C_D*C_L* C_M* C_t = 1500 psi O.K.

Check deflection:

Elastic modulus: E = 1600000 psi*CM* Ct = 1600000 psi

Deflection: D = 5*W*L⁴/(384*E*I) = 0.48 in < L/240 O.K.

Check shear stress

Maximum shear force. V = W*L/2 = 3840 lb

Shear stress, fv = V/bd = 46 psi

Conservatively assume shear stress factor, C_H = 1

Allowable shear stress, Fv = 90 psi * C_D*C_M* C_t*C_H = 90 psi O.K.

Read also:

Follow our official Facebook page (@civilengineeringbible) and Twitter page (@CivilEngBible) and do not miss the best civil engineering tools and articles!