Reinforced Concrete Beam Design
Courses > Reinforced Concrete Design > Design of Concrete Members > Reinforced Concrete Beam Design Introduction
Introduction
In this article reinforced concret beam design is described in detail with solved examples. Beam design is described more in detail in these articles: Flexural Design of Reinforced Concrete Beams, Serviceability of Reinforced Concrete Beams, and Shear Design of Reinforced Concrete Beams.
 Concepts and Formulas
Concepts and Formulas
Loads (Dead & Live), bending moment, and shear diagram of a concrete beam are shown below respectively:
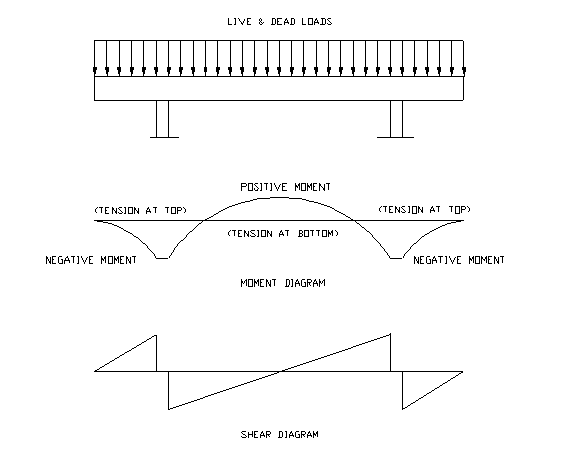
Failure modes and reinforcements
- Concrete is assumed to resist compression only, tension shall be resisted by reinforcements. Reinforcements shall be placed at the side of the beam that has tension. For a simply supported beam, tension is at the bottom of the beam while for a cantilever end, tension is at the top of the beam.
- Shear is at its maximum at the edge of supports. Diagonal shear cracks are normally developed close to the support. Stirrup for shear reinforcement is normally placed vertically to intercept the crack. They are normally closer spaced near the support and gradually spread out toward the center of the beam.

Ultimate Strength design of flexural reinforcements
Design assumption:
- Strain distribute linearly across the section.
- Concrete resists only compressive stresses.
Therefore, the stress distribution across the section of the beam is as shown below:
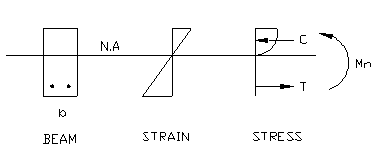
At an ultimate strain of 0.003, the stress at extreme fiber of the beam reaches ultimate strength of concrete fc’. The distribution of the compressive stresses is a complex curve. For calculation purpose, a stress block of 0.85fc’ spread over a depth, a, is used. Therefore, the total compressive stress in a rectangular beam is
C = 0.85fc’ab
Where b is the width of the beam.

At ultimate stress situation, the concrete at top portion is subjected to compression. The compressive stresses distribute uniformly over a depth a. The resultant of compressive stress, C is located at a distance, a/2, from the top surface. The tensile force is taken by rebars at an effective distance, d, from the top surface. By equilibrium, the tensile force is equal to the compression resultant,
T = Asfy = C = 0.85f’c ab
where fy is the yield strength of reinforcing steel and As is the area of steel. Therefore,
The depth of stress block,
a = Asfy/(0.85f’c b), or a = Asfyd/(0.85f’c bd),
Let the reinforcement ratio, r = As/bd, then
a = rfyd/0.85f’c
Let m = fy/0.85f’c , then, a = rdm..The nominal moment strength of the section,
Mn = C (d-a/2) = 0.85f’c ab(d-a/2)
Then, The nominal moment strength of the section,
Mn = Asfy (d-a/2) = Asfy (d-rdm/2) = Asfy d- Asfy drm/2
ACI code requires that the factored moment,
Mu £ f Mn
Where, f = 0.9, is the strength reduction factor for beam design. Let Mu = f Mn , We have Mu = f (Asfy d- Asfy drm/2)
Divide both side by bd2, we have Mu/fbd = (As/bd)fy -(As/bd) fy rm/2) = rfy - fy r2m/2)
Let Rn = Mu/fbd2, and we can rewrite the equation as
r2(m/2) - r - Rn/fy = 0
Solving the equation, the reinforcement ratio,
r = (1/m)[1-(1-2mRn/fy)1/2]
The area of reinforcement is As = rbd
Ductile and brittle failures, Balance condition, Maximum and minimum reinforcement ratio
There are two situations when a reinforced concrete beam fails due to bending. One is when the reinforcing steel reaches its yield stress, fy. The other is when the concrete reaches it maximum compressive stress, f’c. When a reinforced concrete beam fails in yielding of steel, the failure is ductile because the steel can stretch for a long period of time before it actually breaks. When it fails in concrete, the failure is brittle because concrete breaks when it reach maximum strain.
When concrete reaches its maximum strain at the same time as the steel reach is yielding stress, it is called a balance condition. Using a maximum strain, 0.003 of concrete and assume a linear distribution of strain across beam section, one can determine the reinforcement ratio at the balanced condition. The reinforcement ratio based on ACI code is
rb = (0.85f’c/fy) b1 [87000/(87000+fy)] [f’c and fy are in psi (lb/in2)]
rb = (0.85f’c/fy) b1 [600/(600+fy)] [f’c and fy are in MPa (MN/m2)]
Where b1 = 0.85 for 4000 psi (30 Mpa) concrete, and reduce 0.05 for each 1000 psi of f’c in excess of 4000 psi.
To ensure a ductile failure of the beam, ACI code limits the maximum reinforcement ratio to 0.75rb. On the other hand, when the amount of steel is too small, the beam will fail when concrete reaches its tensile strength. It needs to have a minimum amount of steel to ensure a ductile failure mode. The minimum reinforcement ratio in ACI code is rmin = 200/fy (psi).
Shear strength of concrete
The direct shear strength according to ACI is
fvc =0.85[1.9Öfc’+2500rw(Vud/Mu)] £ 0.85(3.5Öfc’)
where rw (» 0.002) is reinforcement ratio, Vu is factored shear stress, Mu is factored moment at the critical section. Or
fvc =0.85(2Öfc’)
ACI code requirements for shear reinforcement:
-
When shear stress, vu £ ½ fvc ,no shear reinforcement is required.
- When ½ fvc < vu £ fvc, use minimum reinforcement
Av = 50 bw s /fy
Where s is spacing of web reinforcement, fy is yield strength of steel, Av is cross section area of web reinforcement, bw is width of beam web.
- When fvc < vu , use vu £ f(vc + vs), where vs is shear strength provided by shear reinforcement.
Stirrup reinforcements:
The shear force that is resisted by shear reinforcements is Vs = (Vu - fVc). Normally, stirrup is spaced vertically at a spacing, s, for shear reinforcement. Within an effective depth d, the shear strength provided by Avfyd/s, where Av is area of stirrup, fy is yield strength of reinforcing steel. The shear strength multiply by a reduction factor, f, needs to be larger than Vs. Therefore, Vs = f(Avfyd/s). The spacing of stirrup is calculated as
s = (fAvfyd)/Vs
ACI code requirements for placing stirrups:
-
When ½ fvc < vu £ fvc, max s = d/2 £ 24 in.
-
When fvc < vs £ 4Öfc, max s = d/2 £ 24 in.
- When fvc < vs £ 8Öfc, max s = d/4 £ 12 in.
 Watch Videos
Watch Videos
 Solved sample problems
Solved sample problems
Example 1: Design of a simply supported reinforced concrete beam
Given:
A simply supported reinforced concrete beam is supporting uniform dead and live loads
Design data:
Dead load: 1500 lb/ft
Live load: 800 lb/ft
Length of beam: 20 ft
Width of beam: 16 in
Depth of beam: 24 in
Minimum concrete cover: 1.5 in
Diameter of stirrup, 0.5 in
Compressive strength of concrete: 4000 psi
Yeild strength of steel: 60000 psi
Support column size: 12”x12”
Requirement: Design flexural reinforcement for bending
Solution:
1. Design for longitudinal bars:
Calculate factored moment:
Weight of beam: WB = 150 lb/ft x 1.33 ft x 2 ft = 400 lb/ft
Factored load: Wu = 1.4(400+1500)+1.7(800) = 4020 lb/ft
Factored moment: Mu = (4020)(202)/8 = 201000 ft-lb
Assume the main reinforcement bar is 1" in diameter (#8 bar)
Effective depth: d:24-1.5-0.5-0.5 = 21.5 in
Factor: Rn = (201000)(12)/[(0.9)(16)(21.52)]=362.4 psi,
m = 60000/[(0.85)(4000)]=17.65
Reinforcement ratio
r = (1/m)(1-2mRn/fy)1/2)=0.0064
Minimum reinforcemnet ratio: rmin = 200/fy=0.0033
Maximum reinforcement ratio; rmin = (0.75)(0.85f’c/fy) b1 [87000/(87000+fy)]=0.021
Required reinforcement, As = rbd = 2.2 in2.
Use 4#8 bar area of reinforcement is 0.79 in2x4 = 2.37 in2.
2. Design for shear bars (stirrups):
Calculate factored shear:
Clear distance between support, Ln = 19 ft
Factor shear Vu = WuLn/2 = 38.2 kips
Shear strength of concrete:
fVc = 0.85(2Ö4000) d b = 37 kips
1/2fVc = 18.5 kips
The length that required no shear reinforcement is
L1 = (Ln /2)(18.5/38.2) = 4.6 ft
Distance from center of beam that required minimum reinforcment is
L2 = (Ln/2)( fVc /Vu) = 9.2 ft close to Ln/2 = 9.5 ft
Use #3 stirrup the area of stirrup, area of steel: Av = 2(0.11 in2) = 0.22 in2.
Maximum spacing, s = (0.22 in2)(60000 psi) /[(50 psi)(16 in)] = 16.5 in
Maximum spacing d/2 = 10.75 in (Govern)
Use 6 stirrups at 10.75 inch spacing, with first stirrup at 5". Total length cover by stirrups is Ls = (5)(10.75 in)+5 in = 4.9 ft O.K.
 Download Files
Download Files
 Read also
Read also
- Solution of Maximum Uniformly Distributed Service Live Load That A Beam Can Support Based on Its Flexural Strength
- Types of Foundations From Construction Point of View
- What are beam bridges? Types and Structural elements of a beam bridge
- Flexural Design of Reinforced Concrete Beams
- Difference Between RCC and Prestressed Concrete
 Share
Share
Follow our official Facebook page (@civilengineeringbible) and Twitter page (@CivilEngBible) and do not miss the best civil engineering tools and articles!

