At-Rest State

Courses > Soil Mechanics > Lateral Earth Pressure > At-Rest State

Introduction

Lateral earth pressure is the pressure that soil exerts in the horizontal direction. Retaining and sheet-pile walls, both braced and unbraced excavations, grain in silo walls and bins, and earth or rock contacting tunnel walls and other underground structures require a quantitative estimate of the lateral pressure on a structural member for either a design or stability analysis.

Concepts and Formulas

At-rest earth pressure for normally consolidated soils:

Let us consider a semi-infinite mass of homogeneous, isotropic soil. The word homogeneous means the soil has the same physical properties (for example, unit weight, hydraulic conductivity, shear modulus and shear strength) at every point, and the word isotropic means the directional properties at any point of the soil mass are the same in every direction. This soil deposit has a free surface that is level (horizontal); the soil deposit extends to infinity downward from the free surface and in the directions parallel to the free surface. Vertical and lateral stresses within this deposit are principal stresses, as the shear stresses in horizontal and vertical planes are clearly zero.

This soil deposit idealization allows us to obtain very important results. If we assume that the soil deposit has not been disturbed after formation, the soil is said to be in a state of rest. For active and passive states of soil see Rankine earth pressure theory, and/or Coulomb earth pressure theory.

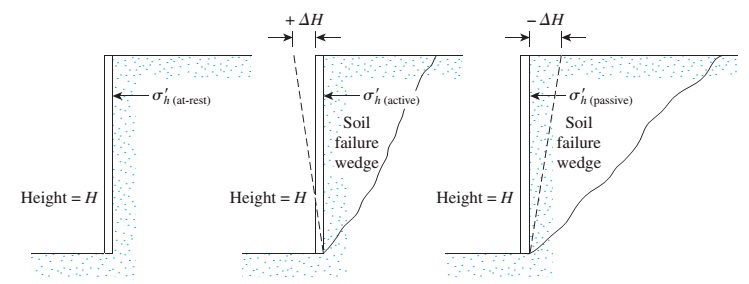
Figure 1. Illustration of nature of lateral earth pressure on a retaining wall at rest, active, and passive states.

The coefficient of lateral earth pressure at rest is the ratio of effective horizontal stress to the effective vertical stress (not total stresses):

$K_{0}=frac{sigma '_{h}}{sigma '_{v}}$

The equation above relates EFFECTIVE stresses not TOTAL stresses! Thus, for calculation of horizontal total stress in presence of ground water table, first effective vertical stress must be calculated then based on At-rest, Rankine, or Coulomb theory (whichever is appropriate), horizontal effective stress will be calculated. Summing the effective horizontal stress with pore water pressure at that point will result in total horizontal stress.

It is a very important quantity that appears often in geotechnical design. For a purely frictional soil, with strength parameters c= 0 and non-zero friction angle, Jacky (1944) established an empirical relationship between K₀ and friction angle:

$K_{0}=1-sinphi$

An alternative expression for K₀ can also be obtained from elasticity, in which case K₀ is related to the Poisson's ratio of the soil through

$K_{0}=frac{ u}{1- u}$

At-rest earth pressure for overconsolidated soils:

Equations above only apply to the normally consolidated soils. Brooker and Irelan (1965) investigated the effects of stress history on K₀, arriving at the following equation:

$K_{0,OC}=K_{0, NC}sqrt{OCR}$

where OCR = overconsolidation ratio, defined as the ratio of preconsolidation pressure, which is the maximum vertical effective stress ever experienced by the soil element, to the current vertical effective stress:

$OCR=frac{sigma'_{vp}}{sigma'_{v}}$

For cohesive soils (Clays):

Cohesion does not have any contribution to the horizontal stresses while the soil is at-rest.

Watch Videos

Collapse of a building due to unsafe excavation

Solved sample problems

Solved problem of the "at-rest" lateral earth pressure upon an unyielding wall

Example 1: Calculation of the at-rest earth pressure coefficient

Required:

For a normally consolidated cohesionless soil with friction angle of 30 degrees, calculate the at-rest value of the earth pressure coefficient, K:

Solution:

$K_{0}=1-sinphi=1-sin30degree = 0.5$

Download Files

No files available for this topic. Suggest one!

Read also

Follow our official Facebook page (@civilengineeringbible) and Twitter page (@CivilEngBible) and do not miss the best civil engineering tools and articles!