Introduction to Finite Elements And the Big Picture

Courses > Finite Elements Method > Basics of Finite Elements > Introduction to Finite Elements And the Big Picture

---

For so many Finite Element Codes in MATLAB including 1D, 2D, and 3D codes, trusses, beams, solids, large deformations, contact algorithms and etc. you can visit matlab-fem.com

Introduction

Application of physical principles, such as mass balance, energy conservation, and equilibrium, naturally leads many engineering analysis situations into differential equations. The exact solutions for differential equations are not applicable to many practical problems because either their governing differential equations does not have an exact solution or they involve complex geometries.

The finite element method is one of the numerical methods for obtaining approximate solution of ordinary and partial differential equations. It is especially powerful when dealing with boundary conditions defined over complex geometries that are common in practical applications.

---

Concepts and Formulas

 

Complete solution procedure:

The approximate solution of any problem governed by a differential equation can be obtained by using the element equations by following the usual finite element steps:

1. Development of element equations
2. Discretization of solution domain into a finite element mesh
3. Assembly of element equations
4. Introduction of boundary conditions
5. Solution for nodal unknowns
6. Computation of solution and related quantities over each element

 

Advantages of using Finite Element Method:

The subdivision of a whole domain into simpler parts has several advantages:

• Accurate representation of complex geometry; while most analytical solutions are restricted to simplified geometries.
• Inclusion of dissimilar material properties; while most analytical methods are applicable to homogeneous materials.
• Easy representation of the total solution
• Capture of local effects.

 

Structural element types:

1. One-dimensional (1D)
   1. Spring (rod) elements
   2. Beam elements 
2. Two-dimensional (2D)
   1. Membrane : in-plane loads only
   2. Shell : in-plane and bending moments
   3. Shear panel : shear loads only
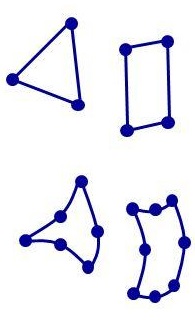
3. Three-dimensional (3D)
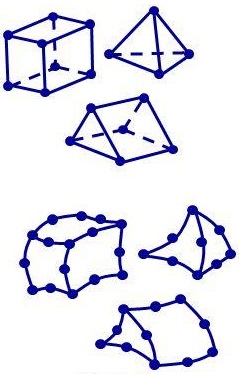
   1. Solid elements

 

---

Watch Videos

---

Solved sample problems

 

---

Download Files

---

Read also

• Free download MATLAB file for finite element analysis of plane trusses + solved example + visualization, including temperature changes and initial strains
• What is Geotechnical Engineering? Subtopics, Salaries, Books, Journals, ...
• Top software for Geotechnical Engineers
• AISC 341-05 requirements for special plate shear walls
• How to read civil engineering drawings?

---

Share

Follow our official Facebook page (@civilengineeringbible) and Twitter page (@CivilEngBible) and do not miss the best civil engineering tools and articles!