Meyerhofs Method

Courses > Foundation Analysis and Design > Bearing Capacity of Shallow Foundations > Meyerhofs Method

---

Introduction

In geotechnical engineering, bearing capacity is the capacity of soil to support the loads applied to the ground. The bearing capacity of soil is the maximum average contact pressure between the foundation and the soil which should not produce shear failure in the soil. Ultimate bearing capacity (q_f) is the theoretical maximum pressure which can be supported without failure; allowable bearing capacity (q_a) is the ultimate bearing capacity divided by a factor of safety. Sometimes, on soft soil sites, large settlements may occur under loaded foundations without actual shear failure occurring; in such cases, the allowable bearing capacity is based on the maximum allowable settlement.

» Try our free powerful online bearing capacity calculator «

There are three modes of failure that limit bearing capacity: general shear failure, local shear failure, and punching shear failure.

 

---

Concepts and Formulas

Meyerhof's bearing capacity theory:

Meyerhof (1963) proposed a formula for calculation of bearing capacity similar to the one proposed by Terzaghi but introducing further foundation shape coefficients.
He introduced a coefficient s_q that multiplies the N_q  factor, depth factors  d_i and inclination factors i_i  depth factors di and inclination factors ii for the cases where the load line is inclined to the vertical. 

 

Meyerhof’s general bearing capacity equations

Meyerhof provided two general equations - one for the case when the resultant load at the bearing level (Qb) is vertical (no horizontal component), and one for the case when Qb is inclined from vertical (can be resolved into vertical and horizontal components) with the horizontal component of load in the direction of the width of the footing.

Vertical load:

Q_b = c N_c S_c d_c + q₀ N_q S_q d_q + 0.5 g B N_g S_g d_g

Inclined load:

Q_b = c N_c d_c i_c + q₀ N_q d_q i_q + 0.5 g B N_g d_g i_g 

where q₀ is the vertical stress at the bearing level outside the footprint of the foundation (called the surcharge pressure). q₀ should be the total vertical stress for total stress strength parameters, and the effective vertical stress for effective strength parameters. The value of g to be used in the above equations depends on the depth of the groundwater table  relative to the depth of embedment of the foundation. See how ground water level can affect unit weight.

Meyerhof's bearing capacity factors

Nc, Nq, Nr:  Meyerhof’s bearing capacity factors depend on soil friction angle, f.

N_q = e^ptanf tan²(45+f/2)

N_c = cot f ( N_q – 1)

Ng = (N_q-1) tan (1.4f)

S_c, S_q, S_g: shape factors

d_c, d_q, d_g: depth factors

i_c, i_q, i_g: incline load factors

Friction angle	Shape factor	Depth factor	Incline load factors
Any f	Sc=1+0.2Kp(B/L)	dc=1+0.2ÖKp (D/B)	ic=iq=(1-q/90°)2
f = 0	Sq=Sg=1	dq=dg=1	ig=1
f³10°	Sq=Sg=1+0.1Kp(B/L)	dq=dg=1+0.1ÖKp (D/B)	ig=(1-q/f)2

 

C: Cohesion of soil

g: unit weight of soil (See how ground water level can affect it)

D: depth of footing

B, L: width and length of footing

K_p = tan²(45+f/2), passive pressure coefficient.

q = tan^-1(Q_h/Q_v) = angle of the load in degrees

 

The table shown below can be used to approximately check your calculation of the main bearing capacity factors (Nc, Nq, and Ng) using Meyerhof’s method. It is, of course, better and more accurate to check it with our free online bearing capacity calculator for shallow foundations.

Table 1: Meyerhof’s bearing capacity factors

f	Nc	Nq	Nr
0	5.1	1	0
5	6.5	1.6	0.1
10	8.3	2.5	0.4
15	11	3.9	1.2
20	14.9	6.4	2.9
25	20.7	10.7	6.8
30	30.1	18.4	15.1
35	46.4	33.5	34.4
40	75.3	64.1	79.4

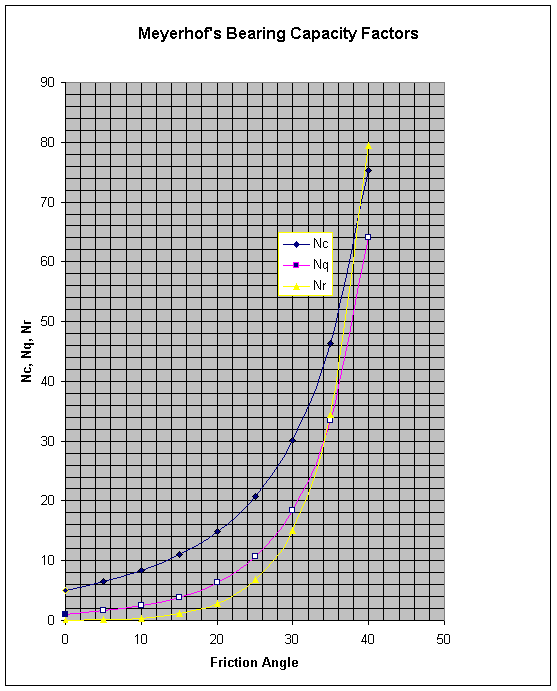
Figure 1: Meyerhof’s bearing capacity factors.

 

 

---

Watch Videos

---

Solved sample problems

Example 1: Strip footing on clayey sand (English units)

Given:

• Soil properties:

• Soil type: clayey sand.

• Cohesion: 500 lbs/ft²

• Cohesion: 25 degree

• Friction Angle: 30 degree

• Unit weight of soil: 100 lbs/ft³

• Expected footing dimensions:

3 ft wide strip footing, bottom of footing at 2 ft below ground level

• Factor of safety: 3

Requirement: 

Determine allowable soil bearing capacity using Meyerhof’s equation.

Solution:

Determine ultimate soil bearing capacity using Meyerhof’s bearing capacity equation for vertical load.

Passive pressure coefficient

Kpr = tan²(45+f/2) = tan²(45+25/2) = 2.5

 Shape factors:

Sc=1+0.2Kp(B/L) = 1+0.2*2.5*(0)=1

Sq=Sg=1+0.1Kp(B/L) = 1+0.1*2.5*(0) = 1

Depth factors:

Dc=1+0.2ÖKp (B/L) = 1+0.2*Ö2 (0) = 1

Dq=Dg=1+0.1ÖKp (D/B) = 1+0.1*Ö2.5 (3/3) = 1.16

From Table 1 or Figure 1, Nc = 20.7, Nq = 10.7, Nr = 6.8 for f = 25 degree

Qu = c Nc Sc Dc + g D Nq Sq Dq + 0.5 g B Ng Sg Dg

= 500*20.7*1*1 +100*3*10.7*1*1.16+0.5*100*3*6.8*1*1.16

=  15257 lbs/ft²

Allowable soil bearing capacity,

Qa = Qu / F.S. = 15257 / 3 = 5085 lbs/ft² @ 5000 lbs/ft²

 

Example 2: Rectangular footing on sandy clay (English units)

Given:

• Soil properties:

• Soil type: sandy clay

• Cohesion: 500 lbs/ft²

• Friction Angle: 20 degree

• Unit weight of soil: 100 lbs/ft³

• Expected footing dimensions:

8 ft by 4 ft rectangular footing, bottom of footing at 3 ft below ground level.

• Factor of safety: 3

Requirement: 

Determine allowable soil bearing capacity using Meyerhof’s equation.

Solution:

Determine ultimate soil bearing capacity using Meyerhof’s bearing capacity equation for vertical load.

Passive pressure coefficient

Kpr = tan²(45+f/2) = tan²(45+20/2) = 2.

Shape factors:

Sc=1+0.2Kp(B/L) = 1+0.2*2*(4/8)=1.2

Sq=Sg=1+0.1Kp(B/L) = 1+0.1*2*(4/8) = 1.1

Depth factors:

Dc=1+0.2ÖKp (B/L) = 1+0.2*Ö2 (4/8) = 1.14

Dq=Dg=1+0.1ÖKp (D/B) = 1+0.1*Ö2 (3/4) = 1.1

From Table 1 or Figure 1, Nc = 14.9, Nq = 6.4, Nr = 2.9 for f = 20 degree

Qu = c Nc Sc Dc + g D Nq Sq Dq + 0.5 g B Ng Sg Dg

= 500*14.9*1.2*1.14 +100*3*6.4*1.1*1.1+0.5*100*4*2.9*1.1*1.1

=  13217 lbs/ft²

Allowable soil bearing capacity,

Qa = Qu / F.S. = 13217 / 3 = 4406 lbs/ft² @ 4400 lbs/ft²

 

Example 3: Square footing with incline loads (English units)

Given:

• Soil properties:

• Soil type: sandy clay

• Cohesion: 1000 lbs/ft²

• Friction Angle: 15 degree

• Unit weight of soil: 100 lbs/ft³

• Expected footing dimensions:

8 ft by 8 ft square footing, bottom of footing at 3 ft below ground level.

• Expected column vertical load = 100 kips

• Expected column horizontal load = 20 kips

• Factor of safety: 3

Requirement: 

Determine allowable soil bearing capacity using Meyerhof’s equation.

Solution:

Determine ultimate soil bearing capacity using Meyerhof’s bearing capacity equation for vertical load.

Passive pressure coefficient

Kpr = tan²(45+f/2) = tan²(45+15/2) = 1.7

Shape factors:

Sc=1+0.2Kp(B/L) = 1+0.2*1.7*(8/8)=1.34

Sq=Sg=1+0.1Kp(B/L) = 1+0.1*1.7*(8/8) =1.17

Depth factors:

Dc=1+0.2ÖKp (B/L) = 1+0.2*Ö1.7 (8/8) = 1.26

Dq=Dg=1+0.1ÖKp (D/B) = 1+0.1*Ö1.7 (3/8) = 1.05

Incline load factors:

q = tan^-1 (20/100) = 11.3°

Ic=Iq=(1-q/90°)2=(1-11.3/90)2= 0.76

Ig=(1-q/f)2=(1-11.3/15)2=0.06

From Table 1 or Figure 1, Nc = 11, Nq = 3.9, Nr = 1.2 for f = 15 degree

Qu = c Nc Sc Dc Ic + g D Nq Sq Dq Iq + 0.5 g B Ng Sg Dg Ig

= 500*11*1.34*1.26*0.76+100*3*3.9*1.17*1.05*0.76+0.5*100*8*1.17*1.05*0.06

=  8179 lbs/ft²

Allowable soil bearing capacity,

Qa = Qu / F.S. = 8179 / 3 = 2726 lbs/ft² @ 2700 lbs/ft²

 

---

Download Files

---

Read also

• Different Concrete Prestressing Methods
• Free Download Portal Method Analyzer
• What Are Precast Segmental Bridges. Types and pros and cons of Precast Segmented Bridges
• Introduction to Finite Elements And the Big Picture
• Shaft Resistance of Piles

---

Share

Follow our official Facebook page (@civilengineeringbible) and Twitter page (@CivilEngBible) and do not miss the best civil engineering tools and articles!