Shaft Resistance of Piles

Courses > Foundation Analysis and Design > Bearing Capacity of Piles (Deep Foundations) > Shaft Resistance of Piles

Introduction

A deep foundation is a type of foundation which transfers building loads to the earth farther down from the surface than a shallow foundation does, to a subsurface layer or a range of depths.

A pile is typically a vertical structural element of a deep foundation, driven or drilled deep into the ground at the building site.

Ultimate bearing capacity of piles is the sum of its skin resistance and tip resistance:

$Q_{ult}=Q_{tip,ult}+Q_{sL}=q_{tip-ult}A_b+sum q_{si}A_{si}$

where Q_tip,ult = tip resistance; Q_sL = skin resistance; q_tip-ult = bearing stress; A_b = area of pile tip; q_si = skin friction of i^thlayer; A_si = skin area in contact with i^th layer;

Concepts and Formulas

There are numerous methods that have been used over the years to estimate shaft resistance. A few of these methods are illustrated in this section.

Granular Soils and Drained Clays (Long-term clays):

K-δ Method:

$q_{sL}=K sigma '_{v0}tandelta$

K and δ are usually estimated based on the type of pile and the characteristics of the soil.
Here are some methods to estimate these two parameters.

â–º Estimate K:

1- Stas and Kulhawy method:

Foundation type and methd of installation	Ratio of horizontal soil stress coefficient to in-situ value, K/K0
Jetted pile	1/2 to 2/3
Drilled shaft, cast-in-place	2/3 to 1
Driven pile, small displacement	3/4 to 5/4
Driven pile, large displacement	1 to 2

2- Sowers method:

Foundation type	Ratio of horizontal soil stress coefficient to in-situ value, K/K0
Foundation type	Loose sand (Dr < 30%)	Dense sand (Dr > 70%)
Jetted piles	0.5 to 0.75	0.5 to 1.0
Drilled piles	0.75 to 1.5	1 to 2
Driven piles	2 to 3	3 to 4

â–º Estimate δ

1- Stas and Kulhawy method:

Interface materials	Ratio of interface angle of friction to soil angle of friction δ/φ	Typical field analogy
sand/rough concrete	1.0	cast-in-place
sand/smooth concrete	0.8 to 1.0	precast
sand/rough steel	0.7 to 0.9	corrugated
sand/smooth steel	0.5 to 0.7	coated
sand/timber	0.8 to 0.9	pressure-treated

Undrained Saturated Clays (Short-term clays):

alpha method:

$q_{sL}=alpha S_u$

obtain α using the following equation from Kulhawy

$alpha = 0.21+0.26frac{P_a}{S_u}leq1$

where Pa = atmospheric pressure; Su = undrained shear strength

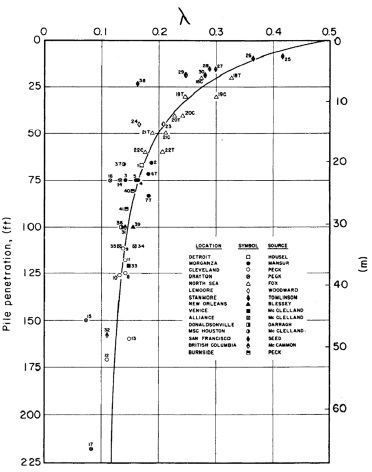
lambda method:

$q_{sL}=lambda(q+2S_u)$

where q is the mean effective vertical stress over the embedded pile length and λ is obtained from the figure below (from Kulhawy). According to Kulhawy, the values of λ shown in the figure below are valid only for steel pipe piles. Limited research has shown that λ for drilled shafts (typically less than 20 ft deep) is on the order of about 1/3 to 2/3 of the values shown in the figure below.

Direct Estimates from In Situ Tests:

From the CPT test, pile shaft resistance can be determined from either the sleeve friction (fs) or the tip resistance (qc):

$q_{sL}=f_s$

$q_{sL}= ho q_c$

where ρ is the friction ratio. For driven piles, the value of rho can be estimated from either of the following equations:

$ho = 0.11(10)^{-1.3tanphi}$

$ho = frac{3}{I_{rr}}$

Values of ρ for drilled shafts are 1/3 to 1/2 the values shown in the two equations above.

Meyerhof recommended the following equations for shaft resistance in high and low
displacement piles:
High displacement piles:

$q_{sL}=0.02p_aN_{60}$
Low displacement piles:

$q_{sL}=0.01p_aN_{60}$
For driven piles in sand, Briaud suggested that:

$q_{sL}=0.224p_a(N_{60})^{0.29}$

Watch Videos

No videos available for this topic. Suggest one!

Solved sample problems

Download Files

No files available for this topic. Suggest one!

Read also

Follow our official Facebook page (@civilengineeringbible) and Twitter page (@CivilEngBible) and do not miss the best civil engineering tools and articles!